21.6 Große Zahlen * 
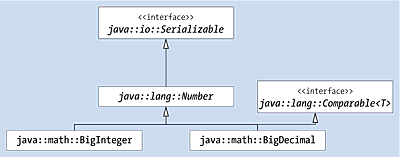
Die feste Länge der primitiven Datentypen int, long für Ganzzahlwerte und float, double für Fließkommawerte reicht für diverse numerische Berechnungen nicht aus. Besonders wünschenswert sind beliebig große Zahlen in der Kryptografie und präzise Auflösungen in der Finanzmathematik. Für solche Anwendungen gibt es im math-Paket zwei Klassen: BigInteger für Ganzzahlen und BigDecimal für Gleitkommazahlen (siehe Abbildung 21.1).
Abbildung 21.1 Die Vererbungsbeziehung von »BigInteger« und »BigDecimal«
21.6.1 Die Klasse BigInteger 
Mit der Klasse BigInteger ist es uns möglich, beliebig genaue Ganzzahlen anzulegen und zu verwalten und mit ihnen zu rechnen. Die BigInteger-Objekte werden dabei intern immer so lang, wie die entsprechenden Ergebnisse Platz benötigen (engl. infinite word size). Die Berechnungsmöglichkeiten gehen dabei weit über die der primitiven Typen hinaus und bieten des Weiteren viele statische Methoden der Math-Klasse. Zu den Erweiterungen gehören modulare Arithmetik, Bestimmung des größten gemeinsamen Teilers (ggT), Pseudo-Primzahltests, Bit-Manipulation und Weiteres.
[zB] Beispiel
Das Quadrat einer nur aus Einsen bestehen Zahl liefert ein interessantes Ergebnis, nämlich eine Zahl, die erstens ein Palindrom[ 277 ](Ein Wort, das sich von vorne wie von hinten gleich liest ) ist und zweitens (bis zur Mitte) hochzählt in der Art 1234…
Listing 21.10 src/main/java/com/tutego/insel/math/BigIntegerDemo.java, main()
BigInteger ones = BigInteger.ONE;
for ( int i = 0; i < 20; i++ ) {
System.out.println( ones + "^2 = " + ones.pow( 2 ) );
ones = ones.multiply( BigInteger.TEN ).add( BigInteger.ONE );
}
Das Ergebnis der Schleife ist:
BigInteger-Objekte sind immer immutable wie Strings. Das Gleiche gilt im Übrigen auch für BigDecimal. Die mathematischen Operationen auf den Objekten liefern also immer neue Objekte.
Konstanten für einige BigInteger-Objekte
In unserem kleinen Beispiel haben wir auf vorhandene BigInteger-Objekte zurückgegriffen und mit ihrer Hilfe neue Objekte gebaut. Insgesamt bietet die Klasse vier Konstanten:
class java.math.BigInteger
extends Number
implements Comparable<BigInteger>
static final BigInteger ZERO
static final BigInteger ONE
static final BigInteger TWO – ab Java 9
static final BigInteger TEN
Im Prinzip lässt sich jedes BigInteger durch mathematische Operationen von diesen Konstanten ableiten. Praktisch ist das aber nicht, daher bietet die Klasse auch Konstruktoren und Fabrikmethoden an.
BigInteger-Objekte erzeugen
Zur Erzeugung stehen uns verschiedene Konstruktoren und eine Fabrikmethode zur Verfügung. Einen parameterlosen Konstruktor gibt es nicht, denn ein leeres immutable BigInteger-Objekt ist wenig sinnvoll.
class java.math.BigInteger
extends Number
implements Comparable<BigInteger>
static BigInteger valueOf(long val)
Statische Fabrikmethode, die aus einem long ein BigInteger konstruiert.BigInteger(String val)
Erzeugt ein BigInteger aus einem Ziffern-String mit einem optionalen Vorzeichen.BigInteger(String val, int radix)
Ein String mit einem optionalen Vorzeichen wird in ein BigInteger-Objekt übersetzt. Der Konstruktor verwendet die angegebene Basis radix, um die Zeichen des Strings als Ziffern zu interpretieren. Für radix > 10 werden die Buchstaben A–Z bzw. a–z als zusätzliche »Ziffern« verwendet.BigInteger(byte[] val)
Ein Byte-Array mit einer Zweierkomplement-Repräsentation einer BigInteger-Zahl im Big-Endian-Format (Array-Element mit Index 0, enthält die höchstwertigen Bits) initialisiert das neue BigInteger-Objekt.BigInteger(byte[] val, int off, int len)
Wie BigInteger(byte[] val), nur ein Teilfeld wird betrachtet.BigInteger(int signum, byte[] magnitude)
Erzeugt aus einem Big-Endian-Betrag bzw. einer Vorzeichen-Repräsentation ein BigInteger-Objekt. signum gibt das Vorzeichen an und kann mit –1 (negative Zahlen), 0 (Null) und 1 (positive Zahlen) belegt werden.BigInteger(int signum, byte[] magnitude, int off, int len)
Wie vorangehender Konstruktor, nur mit Teilfeld.
Neben Konstruktoren, die das Objekt mit Werten aus einem Byte-Array oder String initialisieren, lässt sich auch ein Objekt mit einer zufälligen Belegung erzeugen. Die Klasse BigInteger bedient sich dabei der Klasse java.util.Random. Ebenso lassen sich BigInteger-Objekte erzeugen, die Pseudo-Primzahlen sind.
BigInteger(int numbits, Random rnd)
Liefert eine Zufallszahl aus dem Wertebereich 0 bis 2numBits –1. Alle Werte sind gleich wahrscheinlich.BigInteger(int bitLength, int certainty, Random rnd)
Erzeugt eine BigInteger-Zahl mit der Bit-Länge bitLength (>1), bei der es sich mit gewisser Wahrscheinlichkeit um eine Primzahl handelt. Der Wert certainty bestimmt, wie wahrscheinlich ein Fehlurteil ist. Mit der Wahrscheinlichkeit 1/(2certainty) handelt es sich bei der erzeugten Zahl doch um keine Primzahl. Je größer certainty (und je unwahrscheinlicher ein Fehlurteil) ist, desto mehr Zeit nimmt sich der Konstruktor.
Bei falschen Zeichenfolgen löst der Konstruktor mit String-Parameter eine NumberFormatException aus.
[zB] Beispiel
Gegeben sei eine Zeichenkette, die eine Binärfolge aus Nullen und Einsen kodiert. Dann lässt sich ein Objekt der Klasse BigInteger nutzen, um diese Zeichenkette in ein Byte-Array zu konvertieren. In einem zweiten Schritt soll eine Ausgabe erfolgen:
String s = "11011101 10101010 0010101 00010101".replace( " ", "" );
byte[] bytes = new BigInteger( s, 2 ).toByteArray(); // [158,261,69,69]
System.out.println( Long.toBinaryString( ByteBuffer.wrap( bytes ).getInt() ) );
// 1101110110101010001010100010101
System.out.printf( "%04X", new BigInteger( 1, bytes ) ); // 6ED51515
Die erste Ausgabe benutzt mit ByteBuffer.wrap(bytes).getInt() einen Trick, um die Bytes eines (kleinen) Arrays zu einem int zusammenzubauen. Der Aufruf funktioniert aber nur dann, wenn das Array für ein int genau 4 Byte groß ist – neben getInt() gibt es noch getShort() und getLong() für Arrays der Größe 2 und 8. Für unser Beispiel ist das in Ordnung, weil wir wirklich 4 Bytes haben. Die zweite Ausgabe zeigt noch einen anderen Anwendungsfall für BigInteger, nämlich eine Hex-Ausgabe zu produzieren; das Byte-Array kann eine beliebige Länge haben. Dass es new BigInteger(1, bytes) statt new BigInteger(bytes) heißt, ist wichtig, denn wir wollen für die Hexadezimalausgabe kein Vorzeichen, falls das erste Bit im Byte-Array gesetzt ist und üblicherweise eine negative Zahl anzeigt. Der Format-String %4X füllt die Ausgabe links mit Nullen auf, falls es nötig ist.
Leider existiert noch immer kein Konstruktor, der auch den long-Datentyp annimmt. Seltsam – denn es gibt die statische Fabrikmethode valueOf(long), die BigInteger-Objekte erzeugt. Dies ist sehr verwirrend, da viele Programmierer diese Methoden übersehen und ein String-Objekt verwenden. Besonders ärgerlich ist es dann, einen privaten Konstruktor zu sehen, der mit einem long arbeitet. Genau diesen Konstruktor nutzt auch valueOf(…).
Interne Repräsentation *
Die Implementierung stellt ein BigInteger-Objekt intern wie auch die primitiven Datentypen byte, short, int und long im Zweierkomplement dar. Auch die weiteren Operationen entsprechen den Ganzzahl-Operationen der primitiven Datentypen, wie etwa die Division durch null, die eine ArithmeticException auslöst.
Intern vergrößert ein BigInteger, wenn nötig, den Wertebereich, sodass einige Operationen nicht übertragbar sind. So kann der Verschiebeoperator >>> nicht übernommen werden, denn bei einer Rechtsverschiebung haben wir kein Vorzeichen-Bit im BigInteger. Da die Größe des Datentyps bei Bedarf immer ausgedehnt wird und durch diese interne Anpassung des internen Puffers kein Überlauf möglich ist, muss ein Anwender gegebenenfalls einen eigenen Überlauftest in sein Programm einbauen, wenn er den Wertebereich beschränken will.
Auch bei logischen Operatoren muss eine Interpretation der Werte vorgenommen werden. Bei Operationen auf zwei BigInteger-Objekten mit unterschiedlicher Bit-Länge wird der kleinere Wert dem größeren durch Replikation (Wiederholung) des Vorzeichen-Bits angepasst. Über spezielle Bit-Operatoren können einzelne Bits gesetzt werden. Wie bei der Klasse BitSet lassen sich durch die »unendliche« Größe Bits setzen, auch wenn die Zahl nicht so viele Bits benötigt. Durch die Bit-Operationen lässt sich das Vorzeichen einer Zahl nicht verändern; gegebenenfalls wird vor der Zahl ein neues Vorzeichen-Bit mit dem ursprünglichen Wert ergänzt.
Methoden von BigInteger
Die erste Kategorie von Methoden bildet arithmetische Operationen nach, für die es sonst ein Operatorzeichen oder eine Methode aus Math gäbe:
class java.math.BigInteger
extends Number
implements Comparable<BigInteger>
BigInteger abs()
Liefert den Absolutwert, ähnlich wie Math.abs(…), für primitive Datentypen.BigInteger add(BigInteger val)
BigInteger and(BigInteger val)
BigInteger andNot(BigInteger val)
BigInteger divide(BigInteger val)
BigInteger mod(BigInteger m)
BigInteger multiply(BigInteger val)
BigInteger or(BigInteger val)
BigInteger remainder(BigInteger val)
BigInteger subtract(BigInteger val)
BigInteger xor(BigInteger val)
Bilden ein neues BigInteger-Objekt mit der Summe, Und-Verknüpfung, Und-Nicht-Verknüpfung, Division, dem Modulo, Produkt, Oder, Restwert, der Differenz sowie dem XOR dieses Objekts und des anderen.BigInteger[] divideAndRemainder(BigInteger val)
Liefert ein Array mit zwei BigInteger-Objekten. Im Array, dem Rückgabeobjekt, steht an der Stelle 0 der Wert für this / val, und an der Stelle 1 folgt this % val.BigInteger modInverse(BigInteger m)
Bildet ein neues BigInteger, indem es das aktuelle BigInteger invertiert (entspricht 1/this) und es dann Modulo m nimmt.BigInteger modPow(BigInteger exponent, BigInteger m)
Nimmt den aktuellen BigInteger hoch exponent Modulo m.BigInteger negate()
Negiert das Objekt, liefert also ein neues BigInteger mit umgekehrtem Vorzeichen.BigInteger not()
Liefert ein neues BigInteger, dessen Bits negiert sind.BigInteger pow(int exponent)
Bildet this hoch exponent.int signum()
Liefert das Vorzeichen des eigenen BigInteger-Objekts.BigInteger sqrt()
Liefert die Quadratwurzel und ArithmeticException, wenn die Zahl negativ ist. Seit Java 9.BigInteger[] sqrtAndRemainder()
Liefert ein Array mit zwei Elementen; an erster Position steht die Quadratwurzel (siehe sqrt()), an zweiter Stelle die Differenz aus dem aktuellen Wert und dem Produkt von sqrt(). Seit Java 9.
[zB] Beispiel
Die Wrapper-Klassen Integer oder Long bieten keine Methoden zur Bestimmung eines größten gemeinsamen Teilers oder zum Test auf eine Primzahl. Hier lohnt es, BigInteger einzusetzen. Beispiel: Was ist der ggT von 855 und 99? Antworten wird BigInteger.valueOf( 855 ). gcd( BigInteger.valueOf( 99 ) ).longValueExact() mit 9.
Die nächste Kategorie von Methoden ist eng mit den Bits der Zahl verbunden:
int bitCount()
Zählt die Anzahl gesetzter Bits der Zahl, die im Zweierkomplement vorliegt.int bitLength()
Liefert die Anzahl der Bits, die nötig sind, um die Zahl im Zweierkomplement ohne Vorzeichen-Bit darzustellen.BigInteger clearBit(int n)
BigInteger flipBit(int n)
BigInteger setBit(int n)
Liefern ein neues BigInteger-Objekt mit gelöschtem, gekipptem bzw. gesetztem n-ten Bit.BigInteger shiftLeft(int n)
BigInteger shiftRight(int n)
Schieben die Bits um n Stellen nach links bzw. rechts.int getLowestSetBit()
Liefert die Position des Bits, das in der Repräsentation der Zahl am weitesten rechts gesetzt ist.boolean testBit(int n)
true, wenn das Bit n gesetzt ist.
Folgende Methoden sind besonders für kryptografische Verfahren interessant:
BigInteger gcd(BigInteger val)
Liefert den größten gemeinsamen Teiler vom aktuellen Objekt und val.boolean isProbablePrime(int certainty)
Ist das BigInteger-Objekt mit der Wahrscheinlichkeit certainty eine Primzahl?BigInteger nextProbablePrime()
Liefert die nächste Ganzzahl hinter dem aktuellen BigInteger, die wahrscheinlich eine Primzahl ist.static BigInteger probablePrime(int bitLength, Random rnd)
Liefert mit einer bestimmten Wahrscheinlichkeit eine Primzahl der Länge bitLength.
Des Weiteren gibt es Extraktions- und Konvertierungsmethoden:
double doubleValue()
float floatValue()
int intValue()
long longValue()
Konvertieren das BigInteger in einen double, float, int bzw. long. Es handelt sich um implementierte Methoden der abstrakten Oberklasse Number. Falls die Wertebereiche nicht passen, werden sie passend gemacht. Konvertierungsfehler aufgrund von fehlender Genauigkeit fallen fälschlicherweise nicht auf.[ 278 ](Bei der Konvertierung gibt es bei manchen Werten Probleme mit der Performance. So steht in der Implementierung bei doubleValue() an return Double.parseDouble(this.toString()); »Somewhat inefficient, but guaranteed to work.« )long longValueExact()
int intValueExact()
short shortValueExact()
byte byteValueExact()
Konvertieren den Wert des BigInteger in den gewünschten primitiven Datentyp. Reicht die Genauigkeit nicht aus, folgt eine ArithmeticException. Die xxxValueExact()-Methoden folgen der Bauart der xxxExact()-Methoden aus Math/StrictMath, die bei Überschreitung des Wertebereichs bei Operationen (Addition, Multiplikation …) eine ArithmeticException auslösen.byte[] toByteArray()
Liefert ein Byte-Array mit dem BigInteger als Zweierkomplement.String toString()
String toString(int radix)
Liefern die String-Repräsentation von diesem BigInteger zur Basis 10 bzw. zu einer beliebigen Basis.
[zB] Beispiel
byteValue() und byteValueExact() im Vergleich:
System.out.println( BigInteger.TEN.pow( 3 ).byteValue() );
BigInteger.TEN.pow( 3 ).byteValueExact();
Während Ersteres die Ausgabe »–24« ergibt, folgt bei Letzterem eine »java.lang.ArithmeticException: BigInteger out of int range«, denn natürlich passt 1.000 nicht in ein Byte.
Die letzte Gruppe bilden Vergleichsmethoden:
BigInteger max(BigInteger val)
BigInteger min(BigInteger val)
Liefern das größere bzw. kleinere der BigInteger-Objekte als Rückgabe.boolean equals(Object x)
Vergleicht, ob x und das eigene BigInteger-Objekt den gleichen Wert annehmen. Überschreibt die Methode aus Object.int compareTo(BigInteger o)
Da die Klasse BigInteger die Schnittstelle java.lang.Comparable implementiert, lässt sich jedes BigInteger-Objekt mit einem anderen BigInteger vergleichen. Das ist praktisch, denn BigInteger-Objekte lassen sich so einfach in sortierbare Datenstrukturen legen.
21.6.2 Beispiel: Ganz lange Fakultäten mit BigInteger 
Unser Beispielprogramm soll die Fakultät einer natürlichen Zahl berechnen. Die Zahl muss positiv sein:
Listing 21.11 src/main/java/com/tutego/insel/math/Factorial.java
import java.math.*;
public class Factorial {
static BigInteger factorial( int n ) {
BigInteger result = BigInteger.ONE;
if ( n > 1 )
for ( int i = 1; i <= n; i++ )
result = result.multiply( BigInteger.valueOf(i) );
return result;
}
public static void main( String[] args ) {
System.out.println( factorial(100) );
}
}
Neben dieser iterativen Variante ist eine rekursive denkbar. Sie ist allerdings aus zwei Gründen nicht wirklich gut. Zuerst aufgrund des hohen Speicherplatzbedarfs: Für die Berechnung von n! sind n Objekte nötig. Im Gegensatz zur iterativen Variante müssen jedoch alle Zwischenobjekte bis zum Auflösen der Rekursion im Speicher gehalten werden. Dadurch ergibt sich die zweite Schwäche: die längere Laufzeit. Aus akademischen Gründen soll dieser Weg hier allerdings aufgeführt werden. Es ist interessant, zu beobachten, wie diese rekursive Implementierung den Speicher aufzehrt. Dabei ist es nicht einmal der Heap, der keine neuen Objekte mehr aufnehmen kann, sondern vielmehr der Stack des aktuellen Threads:
Listing 21.12 src/main/java/com/tutego/insel/math/Factorial.java, factorial2()
public static BigInteger factorial2( int i ) {
if ( i <= 1 )
return BigInteger.ONE;
return BigInteger.valueOf( i ).multiply( factorial2( i - 1 ) );
}
21.6.3 Große Fließkommazahlen mit BigDecimal 
Während sich BigInteger um die beliebig genauen Ganzzahlen kümmert, übernimmt BigDecimal die Fließkommazahlen. Wieder sind die Objekte immutable, und es gibt drei Konstanten für die Zahlen BigDecimal.ZERO, BigDecimal.ONE und BigDecimal.TEN.
BigDecimal aufbauen
BigDecimal bietet parametrisierte Konstruktoren für unterschiedliche Typen an, unter anderem long, double und String, und initialisiert damit ein BigDecimal-Objekt.
[»] Hinweis
Bei double ist Obacht geboten, denn während der Compiler bei
new BigDecimal( 1.00000000000000000000000000000000000000000000000000000001 )
das Literal auf den für double gültigen Bereich bringt (1), ist nur
new BigDecimal( "1.00000000000000000000000000000000000000000000000000000001" )
präzise. Das gleiche Phänomen ist bei System.out.println(new BigDecimal(Math.PI)); zu beobachten. Die Ausgabe suggeriert mit
eine hohe Genauigkeit, richtig ist jedoch:
3.141592653589793238462643383279502884197169399375Methoden statt Operatoren
Mit den BigDecimal-Objekten lässt sich nun so rechnen, wie von BigInteger her bekannt. Die wichtigsten Methoden sind:
class java.math.BigDecimal
extends Number
implements Comparable<BigDecimal>
BigDecimal add(BigDecimal augend)
BigDecimal subtract(BigDecimal subtrahend)
BigDecimal divide(BigDecimal divisor)
BigDecimal multiply(BigDecimal multiplicand)
BigDecimal remainder(BigDecimal divisor)
BigDecimal abs()
BigDecimal negate()
BigDecimal plus()
BigDecimal max(BigDecimal val)
BigDecimal min(BigDecimal val)
BigDecimal pow(int n)
Rundungsmodus
Eine Besonderheit stellt die Methode divide(…) dar, die zusätzlich einen Rundungsmodus und optional auch eine Anzahl gültiger Nachkommastellen bekommen kann. Wir betrachten sie zunächst ohne Rundungsmodus:
BigDecimal a = new BigDecimal( "10" );
BigDecimal b = new BigDecimal( "2" );
System.out.println( a.divide(b) ); // 5
Es ist kein Problem, wenn das Ergebnis eine Ganzzahl oder das Ergebnis exakt ist:
System.out.println( BigDecimal.ONE.divide(b) ); // 0.5
Wenn das Ergebnis aber nicht exakt ist, lässt sich divide(…) nicht einsetzen. Die Anweisung new BigDecimal(1).divide( new BigDecimal(3) ) führt zum Laufzeitfehler »java.lang.ArithmeticException: Non-terminating decimal expansion; no exact representable decimal result.«
An dieser Stelle kommen diverse Rundungsmodi ins Spiel, die bestimmen, wie die letzte Ziffer einer Rundung bestimmt werden soll. Sie lassen sich über eine Aufzählung java.math. RoundingMode übermitteln. Folgende Konstanten gibt es:
Konstante in RoundingMode | Bedeutung |
|---|---|
DOWN | Runden nach 0 |
UP | Runden weg von 0 |
FLOOR | Runden nach negativ unendlich |
CEILING | Runden nach positiv unendlich |
HALF_UP | Runden zum nächsten Nachbarn und weg von der 0, wenn beide Nachbarn gleich weit weg sind |
HALF_DOWN | Runden zum nächsten Nachbarn und hin zur 0, wenn beide Nachbarn gleich weit weg sind |
HALF_EVEN | Runden zum nächsten Nachbarn und zum geraden Nachbarn, wenn beide Nachbarn gleich weit weg sind |
UNNECESSARY | Kein Runden, Operation muss exakt sein. |
Tabelle 21.14 Bedeutung der »RoundingMode«-Konstanten
ROUND_UNNECESSARY darf nur dann verwendet werden, wenn die Division exakt ist, sonst gibt es eine ArithmeticException.
Listing 21.13 src/main/java/com/tutego/insel/math/DivideRoundingMode.java, main()
BigDecimal one = BigDecimal.ONE;
BigDecimal three = new BigDecimal( "3" );
System.out.println( one.divide( three, RoundingMode.UP ) ); // 1
System.out.println( one.divide( three, RoundingMode.DOWN ) ); // 0
Jetzt kann noch die Anzahl der Nachkommastellen bestimmt werden:
System.out.println( one.divide( three, 6, RoundingMode.UP ) ); // 0.333334
System.out.println( one.divide( three, 6, RoundingMode.DOWN ) ); // 0.333333
[zB] Beispiel
BigDecimal bietet die praktische Methode setScale(…) an, mit der sich die Anzahl der Nachkommastellen setzen lässt. Das ist zum Runden sehr gut. In unserem Beispiel sollen 45 Liter Benzin zu 1,399 bezahlt werden:
Listing 21.14 src/main/java/com/tutego/insel/math/RoundWithSetScale.java, main()
BigDecimal petrol = new BigDecimal( "1.399" ).multiply( new BigDecimal(45) );
System.out.println( petrol.setScale( 3, RoundingMode.HALF_UP ) );
System.out.println( petrol.setScale( 2, RoundingMode.HALF_UP ) );
Die Ausgaben sind 62.955 und 62.96.
class java.math.BigDecimal
extends Number
implements Comparable<BigDecimal>
BigDecimal divide(BigDecimal divisor, RoundingMode roundingMode)
BigDecimal divide(BigDecimal divisor, int scale, RoundingMode roundingMode)
BigDecimal setScale(int newScale,RoundingMode roundingMode)
21.6.4 Mit MathContext komfortabel die Rechengenauigkeit setzen 
Ein Objekt vom Typ java.math.MathContext gibt für BigDecimal komfortabel die Rechengenauigkeit (nicht die Nachkommastellen) und den Rundungsmodus an. Vorher wurde diese Information, wie das vorangehende Beispiel gezeigt hat, den einzelnen Berechnungsmethoden mitgegeben. Jetzt kann dieses eine Objekt einfach an alle berechnenden Methoden weitergegeben werden.
Die Eigenschaften werden mit den Konstruktoren gesetzt, denn MathContext-Objekte sind anschließend immutable.
class java.math.MathContext
implements Serializable
MathContext(int setPrecision)
Baut ein neues MathContext-Objekt mit angegebener Präzision als Rundungsmodus HALF_UP.MathContext(int setPrecision, RoundingMode setRoundingMode)
Baut ein neues MathContext mit angegebener Präzision und einem vorgegebenen Rundungsmodus vom Typ RoundingMode. Deklarierte Konstanten der Aufzählung sind CEILING, DOWN, FLOOR, HALF_DOWN, HALF_EVEN, HALF_UP, UNNECESSARY und UP.MathContext(String val)
Baut ein neues MathContext-Objekt aus einem String auf. Der Aufbau des Strings entspricht der Formatierung von MathContext toString().toString()
Liefert eine String-Repräsentation, etwa precision=34 roundingMode=HALF_EVEN bei MathContext.DECIMAL128.
Für die üblichen Fälle stehen vier vorgefertigte MathContext-Objekte als Konstanten der Klasse zur Verfügung: DECIMAL128, DECIMAL32, DECIMAL64 und UNLIMITED.
Nach dem Aufbau des MathContext-Objekts wird es im Konstruktor von BigDecimal übergeben.
class java.math.BigDecimal
extends Number
implements Comparable<BigInteger>
BigDecimal(BigInteger unscaledVal, int scale, MathContext mc)
BigDecimal(BigInteger val, MathContext mc)
BigDecimal(char[] in, int offset, int len, MathContext mc)
BigDecimal(char[] in, MathContext mc)
BigDecimal(double val, MathContext mc)
BigDecimal(int val, MathContext mc)
BigDecimal(long val, MathContext mc)
BigDecimal(String val, MathContext mc)
Auch bei jeder Berechnungsmethode lässt sich nun das MathContext-Objekt übergeben:
BigDecimal add(BigDecimal augend, MathContext mc)
BigDecimal subtract(BigDecimal subtrahend, MathContext mc)
BigDecimal divide(BigDecimal divisor, MathContext mc)
BigDecimal remainder(BigDecimal divisor, MathContext mc)
BigDecimal divideToIntegralValue(BigDecimal divisor, MathContext mc)
BigDecimal abs(MathContext mc)
BigDecimal plus(MathContext mc), BigDecimal negate(MathContext mc)
BigDecimal pow(int n, MathContext mc)
BigDecimal round(MathContext mc)
BigDecimal sqrt(MathContext)
21.6.5 Noch schneller rechnen durch mutable Implementierungen 
Die beiden Datentypen BigInteger und BigDecimal sind immutable, was bei vielen Berechnungen zu Laufzeiteinbußen führt. Es gibt in der Open-Source-Welt durchaus Alternativen, etwa http://github.com/tbuktu/bigint oder http://github.com/bwakell/Huldra, das neben der Veränderbarkeit auch andere Algorithmen implementiert. BigInteger wird von Oracle allerdings auch laufend optimiert.


 Java ist auch eine Insel
Java ist auch eine Insel Jetzt Buch bestellen
Jetzt Buch bestellen


